
Está claro que Arenita conoce de epidemiología. En el capítulo 31B de la segunda temporada de la célebre serie animada Bob Esponja, esta ardilla científica texana es víctima de las bromas de toda la ciudad después de una noche de comedia en la que el protagonista la usó como material para sus chistes. No pasaron ni dos días para que todos en Fondo de Bikini los conocieran. Mientras hacía sus compras, Arenita fue capaz de procesar la información y describirla con esa frase contundente:
“La estupidez no es un virus, pero se está propagando como uno…”
Fig 1. Arenita recibe burlas en el supermercado, Bob Esponja (2000)
Para nuestra desgracia, no somos Arenita. Entender cómo es que una infección se propaga entre la gente es un poco más complicado. Necesitamos la ayuda, una vez más, de los modelos matemáticos. Uno de ellos es particularmente útil por ser bueno, bonito, barato y bastante sencillo de entender: el modelo SIR.
El modelo SIR fue desarrollado por un par de científicos llamados W. O. Kermack y G. A. McKendrick en el remoto 1927.1 Es un modelo matemático sencillo y fácil de entender (relativamente). Cada una de las tres letras de esta sigla representa un grupo de personas:
- La S significa susceptible. Son todas las personas candidatas a infectarse.
- La I es de los infectados. Son las personas que ganaron la candidatura.
- La R es para los recuperados. Son las personas que ya pasaron por lo peor.
Una vez que tenemos nuestras categorías, necesitamos saber cómo se relacionan entre sí. Se utilizan dos parámetros:
- β es la tasa de infección o qué tantas personas se van a infectar después de interactuar con un infectado.
- γ es la tasa de recuperación o qué tantas personas se van a curar después de infectarse en un tiempo dado.
Toda esta información queda empaquetada en un amigable sistema de ecuaciones diferenciales ordinarias:

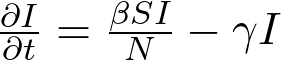
De manera formal, un sistema de ecuaciones diferenciales explica una situación del mundo real a lo largo del tiempo. Pero tranquilos, no es necesario alarmarse, gracias a la computación y sus avances podemos visualizar rápidamente al modelo SIR. Utilizando Python y algunas de sus paqueterías vamos a demostrarlo; primero, vamos a importar las funciones que vamos a necesitar:
import numpy as np #para crear objetos auxiliares
from scipy.integrate import odeint #para resolver las ecuaciones
import matplotlib.pyplot as plt #visualización
La primera función define los objetos auxiliares (np) , la segunda nos ayuda a resolver el sistema de ecuaciones (odeint) y la tercera (plt) a visualizar el modelo; segundo, definimos dentro de una función el sistema de ecuaciones diferenciales ordinarias (EDO):
def SIR(y, t, N, beta, gamma):
S, I, R = y
dS_dt = (-beta * S * I) / N
dI_dt = (beta * S * I) / (N - gamma * I)
dR_dt = gamma * I
return dS_dt, dI_dt, dR_dt
Es importante establecer las condiciones iniciales:
beta = 2.0 #la tasa de infección
gamma = 0.8 # la tasa de recuperación
N = 1000 # la cantidad de personas
t = 50 # la cantidad de días
t = np.linspace(0,t-1,t) # objeto creado para definir del día 1 al t
S0, I0, R0 = N-1, 1, 0 # condiciones iniciales
Resolvemos el sistema de EDO, para más detalles visita la documentación de la función odeint:
y0 = S0, I0, R0 # agrupamos las condiciones iniciales
ret = odeint(SIR, y0, t, args=(N, beta, gamma)) # resolvemos el sistema de EDO
S, I, R = ret.T # los rearreglamos
Ahora visualizamos:
plt.plot(t, S, c='b', label='Susceptibles')
plt.plot(t, I, c='r', label='Infectados')
plt.plot(t, R, c='g', label='Recuperados')
plt.xlabel("Días")
plt.ylabel("No. Personas")
plt.legend()
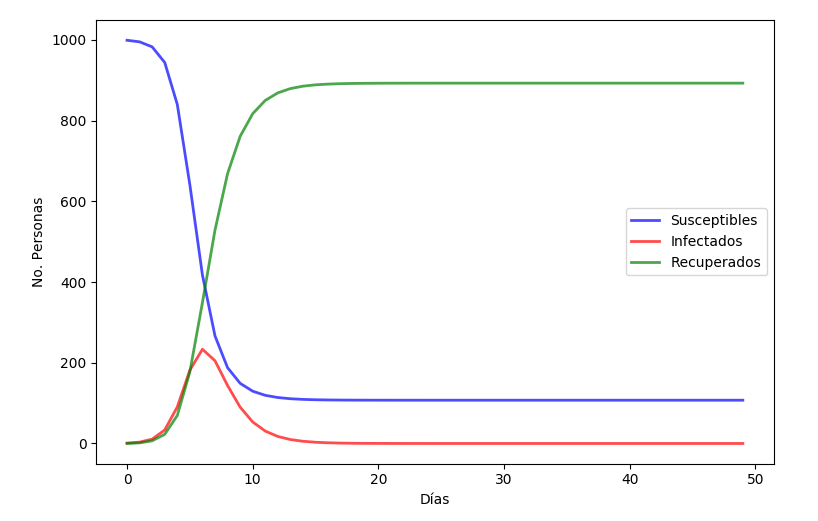
El número de personas vulnerables a la infección disminuirá con el tiempo (línea azul), el número de infectados aumentará hasta llegar a un tope (el pico de la curva, línea roja) para posteriormente disminuir también y el número de recuperados seguirá subiendo hasta que la infección desaparezca (línea verde).
Como todos los modelos, este asume un par de cosas: las personas infectadas lo son desde el primer día y todos los recuperados generan inmunidad. Sabemos que esto no describe a la perfección los modos de cada agente infeccioso, pero nos da una descripción general, muy útil para comenzar a adentrarse en la epidemiología, puesto que la mayoría de las infecciones se comportan más o menos así.
Sea la estupidez, los chistes de ardilla o las infecciones virales, el modelo SIR nos sirve para entender qué tan rápido se va a propagar entre los individuos y qué tan rápido nos vamos a recuperar.
- Kermack WO, McKendrick AG. A contribution to the mathematical theory of epidemics. Proceedings of the Royal Society of London A.1927
Autores: Daniel A. Murillo, Ricardo González y Gener Aviles-R
